Start To Finish is a logical relationship (or dependency) in which a successor activity cannot finish until its predecessor activity has started.
Start to Finish (SF) is one of the four activity relationships of project management. These are used while preparing project schedule. The other three relationships are:
Let us understand SF relationship in greater depth by using examples, Gantt Chart, Network Diagram, and Mathematical formulas.
Start to Finish Relationship (Dependency) in Project Management
As per the PMBOK Guide “Start To Finish is a Logical Relationship in which a Successor Activity cannot finish until a Predecessor Activity has started”.
However a better definition is, “Start to Finish is a Logical Relationship in which finishing event of a Successor Activity is dependent on the starting event of a Predecessor Activity”.
To understand the above definition, let us look at the events of an activity and not the whole activity. The two distinct events of any activity are:
- Start Event (S)
- Finish Event (F)
In SF relationship, the Finish event of the Second Activity is dependent on the Start event of First Activity. The Second Activity is called the Successor and the First Activity is called the Predecessor.
You can also look at Max Wideman’s Glossary for a complete set of PDM definitions.
Note: An activity or task relationship is loosely termed as project dependency. However, these two terms are different. A relationship between two activities can be established only if one activity is dependent on the other. Just like relationships, there are four type of project dependencies.
Start To Finish Examples
Let us consider two activities X and Y. X and Y are predecessor and successor activities respectively. The following examples show SF relationship between X and Y:
- X – Duty of Evening Guard (E), Y – Duty of Morning Guard (M). M cannot Finish her/his duty till E Starts. Simple speaking M cannot abandon the post even if E gets delayed.
- X – Start using New Software System (N), Y – Phase out Old Software System (O). It is assumed that N & O cannot be used in parallel. O cannot be phased out until N is started.
Representation of Start To Finish
Gantt Chart
An SF relationship can be visually depicted using using Time Scaled Bar Charts, which are popularly known as Gantt Charts.
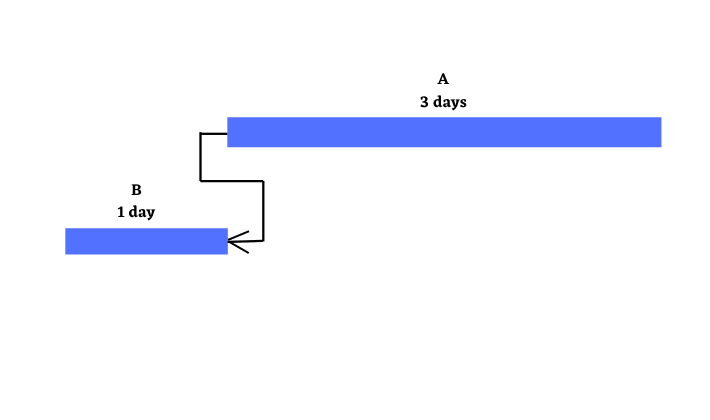
Let us consider two activities A and B.
- Duration of A is 3 days.
- Duration of B is 1 day.
- B has a SF relationship with A
The Gantt Chart below shows SF relationship between A and B.
As per the above diagram B’s Finish is dependent on A’s Start, which means that B can Finish(F) as soon as A Starts(S).
In the above example, A and B together are scheduled to be completed in 4 days.
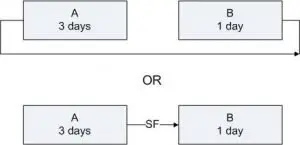
Project Network Diagram
An SF relationship can also be drawn by using Precedence Diagramming Method (PDM), which can be visually depicted by Project Network Diagrams.
Let us again consider the above two activities A and B. The Network Diagram below shows SF relationship between A and B.
Mathematical Formulas
Again considering the above two activities A and B and using 0 method, we can mathematically represent the relationship between A and B as:
B(F) = A(S)
Or, if we use 1 method, we can say that:
B(F) = A(S) – 1
Start to Finish with Lead and Lag
SF relationships can be further modified by introducing Lead and Lag modifiers.
The following Lead and Lag examples use 0 method representation.
Two activities J and K having SF relationship with 1 day of Lead:
K(F) = J(S) – 1 day
Two activities L and M having SF relationship with 2 days of Lag:
M(F) = L(S) + 2 days
Finish to Start is Different from Start to Finish
FS is the most common and natural relationship but it cannot represent every sequence of activities. Although SF can be mathematically transformed to FS to achieve seemingly similar results, the mathematical transformation modifies and tampers the natural logic.
Let’s revisit the Guard example from the previous section to understand why SF is more natural than FS. In the above example, there were two Guards who are doing a shift duty – Evening Guard (E) and Morning Guard (M).
In a natural scenario, M can “Finish” her/his duty only “only after” E “Starts” his/her duty. The critical point here is that “M cannot Finish her/his duty even one minute before E Starts”, otherwise it will be tantamount to abandoning the post. Since M cannot abandon the post, she/he has to guard the post even if E gets delayed in starting her/his duty.
The Finish of M is logically dependent on Start of E.
SF is not a very difficult concept to understand but sometimes it is confused with Finish to Start (FS) relationship. Some authors (incorrectly) claim that FS and SF are essentially same but it is not true.
Over to You
PDM Relationships can be represented by using mathematical equations. However, not all mathematical relationships represent the natural logic. While making a project schedule, you should ensure that all dependencies follow the natural logic and are true in the real world.
Do you think SF relationship is useful in real projects? Have you ever used it in you project(s)? Or have you seen it being used?
I would love to hear from you.
PMP Exam Formulas
I have also compiled a PMP Formulas Cheat Sheet. It contains 45 formulas and 57 abbrviations. It will help you in your exam prep. It is the best and most comprehensive cheat sheet based on the PMBOK Guide 6th edition. You can download it free of cost for your studies.
If you are looking beyond a cheat sheet, then I would suggest you to buy detailed PMP Exam Formula Study Guide by Cornelius Fichtner. It contains detailed explanations of all the formulas along with examples and 105 practice questions.
Disclosure: This article contains affiliate links - it means that, if you buy from any of these links, then I will receive a small commission that would help me in maintaining this blog for free. However, for you, there is no extra cost. I recommend only those products that I believe will definitely help the certification aspirants.

![start to finish [SF] relationship (dependency) examples in project management](https://www.pmbypm.com/wp-content/uploads/2014/06/start-to-finsh.jpg)







Nice post. SF dependency explained nicely with illustration.
Thanks. I appreciate.
Good article, but one instance that you hadn’t considered in your explanation which is more often used in my arena: When you develop a project schedule with a Finish Date in mind (customer defined requirement for Launch Date). In “working backwards from the end date” planning, the SF dependency is used quite a bit.
If you have a better suggestion than SF dependencies in this scenario, I’d like to hear about it.
Hi Bob,
The relationships do not change whether you “Schedule From Start Date” or “Schedule From Finish Date”. I suspect most of your relationships would be FS. Plese note that these are Logical relationships and not mathematical relationships.
I think you may want to read more about constraints like “As soon as possible” and “As late as possible” if you using a tool like MS Project.
You should also read more about the network diagrams.
BR
Praveen.
Can you give a concrete example in construction wherein the predecessor must start before a successor could finish. I saw one in the internet, eg. the installation of a new pipeline wherein the old pipeline must start to complete the new pipeline. However it did not specified lag scenario, can you illustrate that too?
Also in your Gantt illustration, activity A seems to be the successor making activity B the predecessor.
Hi Joji, Three things:
1. Your example seems to be correct. Let me modify the wordings – stop (finish) using old pipeline immediately after new pipeline starts functioning.
2. For leads and lags look at my articles – https://www.pmbypm.com/project-schedule-leads-and-lags/ and https://www.pmbypm.com/faq-lead-and-lag/
3. Gantt chart is correct – just look at the direction of the arrow. Predecessor and successor are not determined by starting dates but by dependency between them.
BR, Praveen.
I found the very unique and valuable information through the article thanks for sharing such a wonderful piece of knowledgeable information. Worth reading it.
Thanks Sebestine.
Nice articles about the different types of dependencies. I like the format and breakdown of math as well as images. Nice job.
Thanks Chris
thank you
“Y – Start using New Software System (N), Y – Phase out Old Software System (O). It is assumed that N & O cannot be used in parallel. N cannot be started until O is phased out.”
There is likely a typo here (both activities listed as Y) but as described this looks like FS. O being phased out is a (F)inish and N starting is a (S)tart. I think we should say O cannot be phased out until N is started. Rather than saying they cannot be used in parallel we would say that there cannot be a time with no system in operation.
SF relationships do occur but are not all that common and often cause confusing even among experienced PMs.
Thanks Bob.
SF dependency is used where starting of a certain activity is actually depends on successor activity finishing and successor activity is the driver.
Take an example of student preparation task 10 days (A) and Writing Exam 1 day (B), so if you say A—>B is incorrect as student might prepare for the exam, but teacher may decide to postpone the exam. so here the Preparation for exam is not the driving activity but the EXAM (B) drives when student should start preparation. so dependency (A)<—(B) is correct which A needs to start in time to finish B, if Exam dates moves, preparation start automatically moves based on given duration.
For Construction example say you are erecting an equipment from Ground floor to 3rd floor, so lifting the equipment (crane etc. should start when, foundation at 3rd floor is ready) so here Start of lifting is required to Finish the Erection at 3rd floor but whole point is when to start is governed by later activity. you would not want to hire the crane and start lifting, equipment and find later that at point of receive ie 3rd floor there is no one to finish it i.e unload and erect it. So main difference is when to start preceding activity when Finish has its own schedule defined.
Thanks for sharing the examples. Only thing is that successor activity is always dependent on predecessor activity in all four type of relationships.
Hi Praveen,
I think due to lack of good example this topic( SF) has been criticised. Let me give a try.
If ‘Taking off of an aeroplane ‘ is considered as successor and ‘Boarding of passengers ‘ is considered as predecessor then SF RELATIONSHIP can be explained with the constraint , the Boarding must start 45 minutes before take off.
Pilot is CONSTRAINED to wait till 45 minutes are lapsed after predecessor i.e. Boarding I.e. predecessor activity is started. SF relationship with minus sign ( I.e. -45 min ) illustrates the point.
If due to some logistic issues at boarding is delayed by say 10 minutes the take off is also delayed .
Thus predecessor Start controls successors Finsh.
‘Hope this helps.
Regards
Sudhir Fadnavis
SF relationships are not considered useful due to lack of correct example. Generally it’s assumed that FS relationships can take care of the requirements.
I have thought of example to counter this thought process.
Let’s consider a scheduling scenario that defines two activities one of which is ‘Boarding an aeroplane ‘ is predecessor and ‘Taking off the aeroplane’ a successor. The business scenario is predecessor must start , say 45 minutes before successor. SF relation with -45 minutes should take care of the requirements.
Expected counter argument would be why not use FS relationship . Because Captain is not going to wait till Boarding of last passenger. He has to stick to schedule given by control room.
Here even SS relationship with +45 minutes also not useful. The problem here is that in this case predecessor controls successor which is not wanted.
If , for example if there’s reschedule from Airport control room , reschedule will be an issue…
To conclude, SF is needed to ‘foreclose ‘ predecessor as necessary because succssor is The Boss and not the predecessor.
‘Hope I am clear.
Hi Sudhir, Thanks for your comment. If boarding is predecessor and takeoff is successor (as written in your comment) then it is going to be FS relationship. Please read the definition again
Start to Finish is a Logical Relationship in which finishing event of a Successor Activity is dependent on the starting event of a Predecessor Activity.
On the other hand, in FS relationship, the Start event of the Successor is dependent on the Finish event of Predecessor.
Best, Praveen.
Hi Praveen,
Thanks for your prompt feedback. I thought I was wrong in first response hence I had sent the revised one in which I mentioned that only starting of Boarding matters. End of Boarding will happen iff ( if and only if ) THE last passenger boards the plane which is not the case
Further there is no constraint regarding when the successor start ( it could be few hours earlier or could be few minutes before take off , at least theoretically ) thus neither F of predecessor nor S of successor is relevant.
However as mentioned by you , if that example is also wrong, let me think how to redraft the concept.
Regards
Sudhir
Sudhir, I would suggest the following:
1. start with identification of two activities.
2. identify which one these are predecessor and successor.
3. Identify the start event and finish event of these two activities.
4. Finally determine the relationship between the activities.
Best, Praveen.