Using PERT & Standard Deviation For Critical Path Analysis

You would find Program Evaluation & Review Technique (PERT), Critical Path Method (CPM) and Standard Deviation in complete detail this post. IT describes how they are related to each other and how they can be used together for project schedule analysis.

This article assumes that you are already know how to use PERT Formula for doing three point estimation and you are also familiar with Standard Deviation calculations for finding a range of estimates.

In this article I have combined these concepts for determining the project schdule.

How to Use PERT, Standard Deviation and Variance For Doing Critical Path Analysis?

What is Critical Path Method (CPM)?

Critical Path is the Longest Path in a Project Network. Critical Path represents the Shortest Possible Duration of the project. Critical Path can be determined by applying Critical Path Method (CPM) on the Project Network.

How can Critical Path be “Longest” and “Shortest” at the same time? Refer to the 17 Frequently asked Questions on the Critical Path Method to get answer to this question and some other frequently asked questions”.

What is Program Evaluation and Review Technique (PERT)?

PERT is a Three-Point Estimation technique. This technique is based on Beta Distribution and uses 3 different duration estimates to arrive at a final estimate. Since, a single-point estimation is more risk-prone, PERT uses 3  different estimates to arrive at a final estimate. PERT reduces the Risks and improves the accuracy of estimation. You can refer to 3-point estimation is different from PERT… to understand nuances of Three Point Estimation and PERT.

What is Standard Deviation?

In Statistics and Probability Theory, Standard Deviation (SD) measures the amount of Variation from Average or Mean. In current context Average or Mean is represented by Weighted Average calculated using PERT formula.

A low value of SD indicates that data points are very close to the Mean. On the other hand a high value of SD indicates that data points are spread out over a large range.

You can refer to What is Significance of Standard Deviation in PERT formula? to understand how SD can be used to determine the probability of finishing a task within a specified time range.

PERT and CPM are singular concepts. In my previous articles on PERT & CPM were treated as singular concepts. However, PERT & CPM can be combined together to improve Project Schedule Management. Let us understand the combination of PERT & CPM by looking at an example.

PERT CPM Example

Let us consider a Project Network having 3 activities on the Critical Path – Alpha, Bravo and Charlie. Refer to Figure 1 to understand the relationship between the 3 activities.

Refer to Figure 2 to check data values corresponding to the 3 activities shown in figure 1. The Mean in Figure 2 (for each activity) is calculated by using the PERT formula.

E_PERT=(O+P+4×M)/6

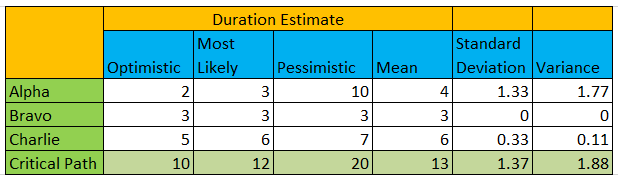
The Standard Deviation (SD) or σ in Figure 2 (for each activity) is calculated by using the following formula.

σ = (P – O)/6

The Variance in Figure 2 (for each activity) is calculated by using the following formula

Var = SQR(σ)

You would notice that (in Figure 2) there are 4 different Duration of Critical Path. The Optimistic, Pessimistic, Most Likely and Mean Duration of the Critical Path are calculated by adding their respective individual values.

Now which of these 4 is the real Critical Path?

There could be only one Longest Duration in a Project. CPM (Critical Path Method) is about Longest Path(s).

Refer to the following figures – Figure 3 to Figure 5. These figures depict Optimistic, Pessimistic and Most Likely Critical Paths. All the figures are drawn using Time Scaled Schedule Network Diagram.

Which of these 3 Paths should be managed by the PM?

If we are using PERT then none of the above Schedules describe the real Critical Path. PERT calculations were done to manage Risks. However, none of the above Schedules manages Risk appreciably. Let us draw a 4th figure using Mean of Estimated Values. Refer to Figure 6 – it depicts the real Critical Path.

So what is the use of Standard Deviation (σ)?

Let us use the Variances  along with the Mean Values in order to manage Risks better.

We have already calculated σ for all 3 activities – Alpha, Bravo & Charlie. We now have to calculate Critical Path σ. Critical Path σ cannot be calculated by simply adding individual σ. As per the Statistics, individual σ cannot be added together. In order to determine Critical Path σ, we have to first find Variance of the Critical Path.

Var (Critical Path) = Var(Alpha)+Var(Bravo)+Var(Charlie)

As per the Statistics, σ can be determined by taking Square Root of Variance.

σ = SQRT(Var)

So, in our case Critical Path σ would be

σ (Critical Path) = SQRT( Var(Alpha)+Var(Bravo)+Var(Charlie) )

Refer again to Figure 2 for all the values. So, in our case, there is a 68.27% likelihood that Project Duration (Critical Path) will come out to be 13±1.37 days. Or, in other words, we can say that there is a 68.27% probability that Project Duration will be between 11.63 days and 14.37 days. Figure 6 shows Critical Path using Mean Duration.

Next step. Let us determine the probability of passing the PMP exam…Good luck to all PMP aspirants!

I hope you would have understood the relationship between CPM and PERT Formulas. You can leave a comment, if you would like to know anything else on this topic.

Related Content

I have compiled another article that provides a quick reference to all the three point estimation formulas. It contains 8 different formulas and 6 different sigma values.

PMP Exam Formulas

I have also compiled a PMP Formulas Cheat Sheet. It contains 45 formulas and 57 abbrviations. It will help you in your exam prep. It is the best and most comprehensive cheat sheet based on the PMBOK Guide 6th edition. You can download it free of cost for your studies.

Download Free PMP Formulas Cheat Sheet

If you are looking beyond a cheat sheet, then I would suggest you to buy detailed PMP Exam Formula Study Guide by Cornelius Fichtner. It contains detailed explanations of all the formulas along with examples and 105 practice questions.

Disclosure: This article contains affiliate links - it means that, if you buy from any of these links, then I will receive a small commission that would help me in maintaining this blog for free. However, for you, there is no extra cost. I recommend only those products that I believe will definitely help the certification aspirants.